Congruência e Aritmética Modular – Teoremas úteis.
Em Teoria dos Números, algo que ajuda muito na hora de resolver problemas é a famosa “aritmética modular”, que é equivalente à análise de restos. Você pode ver o básico sobre aritmética modular e relações de congruência aqui, no post antigo do Eduardo. Entretanto, hoje vamos mais a fundo: saberemos como determinar quais números têm um inverso modular, além de alguns teoremas e aplicações importantes, porém mais recentes. Mas, antes, vamos relembrar o básico:
Definição 1: Dizemos que dois inteiros a,b são congruentes módulo m se m|a – b. (Escrevemos a ≡b (mód m)). Analogamente, se a,b são congruentes módulo m, eles têm o mesmo resto na divisão por m.
Reparem que as relações de congruência satisfazem todas as propriedades básicas de operações com inteiros:
Proposições Básicas: Se a ≡ b mod m e c ≡ d mod m, então a + c ≡ b + d mod m, a – c ≡ b – d mod m, ac ≡ bd mod m.
Exemplo Básico:
Resolução: Essa conta não parece muito “apetitosa” de se fazer. Portanto, vamos apenas analisar os restos das potências de 3 mód 7:
E, assim, temos nossa repetição. Logo, agora nossa tarefa é determinar o resto de
Mas
Logo, como 323 é ímpar, 5323 deve deixar resto 5 módulo 6. Assim, temos que nossa tarefa é equivalente a achar o resto de 35 módulo 7, que sabemos ser 5. Portanto,
Agora, podemos prosseguir à parte interessante:
Teorema de Invertíveis: Um número inteiro a é invertível módulo n quando existe b tal que ab ≡ 1 mod m. Então, todos os números invertíveis módulo m são os coprimos com m (ou seja, mdc(a,m) = 1).
Demonstração: Suponhamos mdc(a,m) ≠ 1, a<m. Então, se
O que significa que uma combinação linear de a,m tem que dar 1. Absurdo, pois a menor combinação linear que pode ocorrer entre dois números é seu mdc, que, neste caso, é diferente de 1. ■
Corolário: Todo inteiro m admite φ(m) invertíveis módulo m, onde φ(m) é o número de primos com m. ■
Com este teorema em mãos, vamos ao famoso
Teorema de Wilson: Seja p primo maior que 2. Então (p – 1)! ≡ -1 mod p.
Demonstração: Temos que todos os inteiros mód p são invertíveis, mas apenas dois destes são o inversos deles mesmos: 1 e -1. Mas isto tem que ser demonstrado:
Se
Então
Mas p é primo, e ambas as parcelas, menores que p. Logo, seu produto tem de ser igual a zero, gerando que x=1 ou x = -1.
Com isso, todos os inteiros módulo p ao serem multiplicados, com exceção do 1 e do -1, encontrarão seu inverso multiplicativo, e resultarão em 1 mod p. Ao multiplicar esses “uns” pelo um e pelo -1, obtemos -1. Mas a multiplicação de todos os inteiros menores de p é justamente (p – 1)!, o que completa a prova. ■
Corolário:
Demonstração: Temos que
Logo,
Como queríamos demonstrar. ■
Com este teorema em mãos, podemos aplicá-lo a alguns problemas:
Problema 1: Mostre que, p primo maior que 3, então
Resolução: Para este problema, precisaremos de um importante lema:
Se o leitor quiser, este pode demonstrá-lo utilizando indução. Porém, para poupar os detalhes da demonstração, prossigamos. Ao diminuir 2, teremos apenas fatores “múltiplos” de p². Isto é óbvio, pois p é primo. Assim, tudo que temos que fazer é demonstrar que
Mas isto é fácil: Reparemos que todos os k’s têm um inverso, digamos, rk. Assim, Podemos escrever
Mas os rk são apenas uma reordenação dos números de 1 a p – 1. Logo, Esta é a soma de todos os quadrados de números de um a n, que se dá por
Logo, no nosso caso,
Que é, de fato, múltiplo de p. ■
É óbvia, depois desse exemplo, a importância dos inversos multiplicativos módulo m. Agora, vamos a mais um teorema que ajuda muito na hora de resolver problemas deste tipo: o teorema de Euler-Fermat.
Teorema de Euler: Seja a um inteiro positivo e m outro inteiro positivo com mdc(a,m) = 1. Então, sempre vale que
Demonstração: Comecemos observando que se  são os números primos com m menores que m, então eles são todos invertíveis, e representam todos os invertíveis módulo m. Logo, se selecionarmos a tal que mdc(a,m) = 1, então
são os números primos com m menores que m, então eles são todos invertíveis, e representam todos os invertíveis módulo m. Logo, se selecionarmos a tal que mdc(a,m) = 1, então  também representará todos os invertíveis módulo m. Assim, se multiplicarmos todos os números deste conjunto e analisarmos o produto módulo m, teremos
também representará todos os invertíveis módulo m. Assim, se multiplicarmos todos os números deste conjunto e analisarmos o produto módulo m, teremos
Como queríamos demonstrar. ■
Corolário (Teorema de Fermat): É válido para todo a que
Demonstração: Para a múltiplo de p, é óbvio. Para todos os outros, como mdc(a,p)=1, então podemos aplicar diretamente o teorema acima para obter ap – 1 ≡ 1 mod p, e, multiplicando por a dos dois lados, obtemos a relação desejada. ■
Agora, vamos ao exemplo ilustrativo:
Problema 2: (OIbM 2001) Demonstrar que para todo n inteiro positivo existe 2m com m inteiro positivos tal que este tenha pelo menos 2n/3 – 1 zeros consecutivos dentre suas n últimas casas decimais.
Resolução: Sabemos que
Pelo teorema de Euler. Assim,
Agora, sabemos que 2n das ultimas casas decimais do número estão ocupadas com algarismos não nulos (na verdade, nem todos são não-nulos, mas eles bloqueiam a nossa sequência de zeros, e é isso que importa). Mas
Logo, eles bloqueiam no máximo n/3 +1 casas do final do número (pois n/3,quando não é inteiro, arredonda a potência de 10 para cima). Logo, Temos que pelo menos 2n/3 – 1 zeros consecutivos serão mantidos.
Ou seja, para todo n inteiro positivo, m = φ(5n) + n = 4.5n – 1 + n satisfaz o enunciado. ■
Observação: Este problema é clássico em teoria dos números; Várias versões envolvendo números de zeros ao final de certa potência de 2 são muito amplamente conhecidas, esta é a generalização deste problema.
Bom, espero que tenham gostado e entendido tudo que foi dito neste post, embora não tenha sido muito detalhado. Se você não está muito familiarizado com congruências, volte ao topo do post e veja o primeiro post sobre congruências, do Eduardo.
Lembre-se! Sua opinião é muito importante para sabermos sobre a qualidade do nosso trabalho. Avalie o post abaixo, não demora nada. Se quiser se expressar mais livremente, os comentários são incentivados por nós, donos do blog! Apenas lembre-se de ser educado na sua crítica ou sugestão.
Fontes:
MARTINEZ, Fabio Brochero, MOREIRA, Carlos Gustavo, SALDANHA, Nicolau, TENGAN, Eduardo. Teoria dos Números: Um passeio com primos e outros números familiares pelo mundo inteiro. Projeto Euclides, Brasil, 2010.

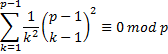


Nenhum comentário:
Postar um comentário